I. Introduction
Despite of the increasing computational capability now available,
molecular modeling and simulation of large, complex systems at atomic level
remains a challenge to computational chemists. At the same time, there is
increasing interest in nanostructured materials, condensed-phase reactions, and
catalytic systems, including designer zeolites and enzymes, and in modeling
systems over longer time scales that reveal new mechanistic details. The
central problem is: can we efficiently accomplish accurate calculations for
large reactive systems over long time scales? As usual, we require advances in
modeling potential surfaces, in statistical mechanical sampling, and in
dynamics. The present article is concerned with the potentials.
Models based on classical mechanical constructs such as molecular
mechanical (MM) force fields1-19 that are based on empirical potentials
describing small-amplitude vibrations, torsions, van der Waals interactions,
and electrostatic interactions have been widely used in molecular dynamics (MD)
simulations of large and complex systems. However, the MM force fields are
unable to describe the changes in the electronic structure of a system
undergoing a chemical reaction. Such changes in electronic structure in
processes that involve bond-breaking and bond-forming, charge transfer, and/or
electronic excitation, require quantum mechanics (QM) for a proper treatment.
However, due to the very demanding computational cost, the application of QM is
still limited to relatively small systems consisting of up to tens or several
hundreds of atoms, or even smaller systems when the highest levels of theory
are employed.
Algorithms that combine quantum mechanics and molecular mechanics provide a solution to this problem. These algorithms in principle combine the accuracy of a quantum mechanical description with the low computational cost of molecular mechanics, and they have become popular in the past decades. The incorporation of quantum mechanics into molecular mechanics can be accomplished in various ways, and one of them is the so-called combined quantum mechanical and molecular mechanical (QM/MM) methodology.20-111
|
|
|
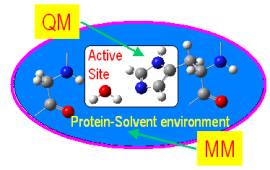
Fig. 1. Illustration for the QM/MM method in the
enzyme system. The active center is treated at the QM level and the
surroundings is treated at the MM
level. |
A QM/MM method (see Fig. 1)
treats a localized region, e.g., the active site and its neighbors in an enzyme (called the primary subsystem, PS), with QM methods and includes the influence of the surroundings (e.g., the protein environment, called secondary subsystem, or SS) at the MM level. The QM/MM energy for the entire system (ES) can be formally defined by
E(QM/MM;ES) = E(QM;PS) + E(MM;SS)
+ E(QM/MM;PS|SS), (1)
i.e., as a summation of the energy of the PS, the energy for the SS, and the interaction energy between them. The relation between ES, PS, and SS is given by
ES = SS + PS. (2)
The PS is also called the QM subsystem (or ¾ sometimes ¾ the MO-subsystem), and the SS is often
called the MM subsystem. The inclusion of the interactions between the active
center and its environment allows a more realistic description of the system,
in comparison with isolated QM calculations on subsystems, which are often
called model systems. Such a
PS-SS coupling is the heart of a QM/MM method.
Recently, there has been much exciting progress on algorithm development,
implementation in programs, and applications of QM/MM methods. In this
contribution, we will briefly review the current status of the most popular
methods for QM/MM calculations, including their advantages and
disadvantages. There are many excellent reviews of QM/MM methods available
in literature.24,36,40,59,76,98,106 The present study will put a
special emphasis on very general link atom methods and discuss various ways to
treat the charge near the boundary.
Mechanical and electrostatic embedding will be contrasted. We will
review some recent tests and applications from our work and that of other
groups and summarize what we learn about QM/MM from these studies. We will
also discuss some available software. Finally, we will present a few
comments about future directions of research in this exciting area.
II. Interactions between the Primary and Secondary Subsystems
The coupling between the primary
system (PS) and the secondary
subsystem (SS) is the heart of a QM/MM
method. The coupling, in general, must be capable of treating both bonded
interactions (bond stretching, bond bending, and internal rotation, sometimes
called valence forces) and non-bonded interactions (electrostatic interaction
and van der Waals interactions). Various QM/MM schemes have been developed to
treat the interactions between the PS and SS.
As might be expected from its
general importance in a myriad of contexts,112 the electrostatic interaction is the key element of the coupling.
Depending on the treatment of the electrostatic interaction between the PS and
SS, the QM/MM schemes can be divided into two groups, the group of mechanical
embedding and the group of electric embedding.45 A mechanical embedding (ME) scheme performs
QM computations for the PS in the absence of the SS, and treats the
interactions between the PS and SS at the MM level. These interactions usually
include both bonded (stretching, bending, and torsional) interactions and
non-bonded (electrostatic and van der Waals) interactions. The original
integrated molecular-orbital molecular-mechanics (IMOMM) scheme30-32 by Morokuma and coworkers, which is also known as the two-layer
ONIOM(MO:MM) method, is an ME scheme.
In an electrostatic embedding
(EE) scheme, also called electric embedding, the QM computation for the PS is
carried out in the presence of the SS by including terms that describe the
electrostatic interaction between the PS and SS as one-electron operators to
enter the QM Hamiltonian. Usually the SS atoms are conveniently represented by
atomic-centered partial point charges in the effective QM Hamiltonian, because
most popular MM force fields like CHARMM or OPLS-AA have developed extensive
sets of atomic-centered partial point charges for calculating electrostatic interactions
at the MM level. However, more complicated representations involving
distributed multipoles have also been attempted.79,80 The bonded (stretching, bending, and
torsional) interactions and non-bonded van der Waals interactions between the
PS and SS are retained at the MM level.
A comparison for between the ME and EE schemes are presented in Table 1, and it will be discussed in detail in Subsections II.A and II.B.
Table 1. A Comparison between the Mechanical Embedding (ME) and Electrostatic Embedding (EE) Schemes
|
|
ME |
EE |
|
Electrostatic interaction between the
primary system (PS) and the secondary system (SS) |
Handled in the standard MM way |
Treated by
including certain one-electron terms in the QM Hamiltonian |
|
Advantage |
Simple |
1. Do not need electrostatic MM parameters for PS atoms, which may change their character during the simulation 2.
The electronic structure of the PS adjusts to the
charge distribution in the SS |
|
Disadvantage |
1. An accurate set of electrostatic MM parameters is often not available for PS atoms 2.
Ignores the potential perturbation of the electronic
structure of the PS by the charge distribution of the SS |
1.
More
computational effort 2.
Need to construct an appropriate representation for the
charge distribution in the SS |
II.A. Mechanical Embedding?
The key difference between an ME scheme and an EE scheme is how they treat the electrostatic interaction between PS and SS. An ME scheme handles the interaction at the MM level, which is simpler. However, such a treatment has drawbacks. First, the treatment requires an accurate set of MM parameters such as atom-centered point charges for both the PS and SS. It is relatively easier to get such parameters for the SS, and the problem with getting such parameters for the PS, where reactions are taking place, was the central reason for moving from MM to QM in the first place. Since the charge distribution in the PS usually changes as reaction progresses, the error in using a single set of MM parameters could be very serious. The second drawback of an ME scheme is that it ignores the potential perturbation of the electronic structure of the PS due to the electrostatic interaction between the PS and SS. The atom-centered charges in the SS polarize the PS and alter its charge distribution. This is especially a problem if the reaction in the PS is accompanied by charge transfer. Another problematic situation would be a system (e.g., an open-shell system containing transition metals) having several electronic states close in energy, for which the polarization could change the energetic order of these states, e.g., predicting a different ground state with a different charge and/or spin distribution.
To deal with the lack of accurate MM electrostatic parameters for the PS atoms during a reaction, one might think of obtaining these parameters dynamically as the reaction progresses, e.g., deriving atom-centered point charges for the PS atoms when the system evolutes along the reaction path. This idea works in principle, but in practice, it requires a large PS to achieve the desired accuracy due to the second drawback of ME schemes, which was just discussed above. That is, the PS system must be large enough to assure that its calculated charge distribution is converged with respect to the location of the QM/MM boundary. Moreover, an accurate and fast algorithm is necessary to derive the MM electrostatic parameters on the fly (with no or only a little calibration by experimental data or validation by doing pure MM simulation). These requirements will apparently increase the computational effort considerably.
This problem motivates consideration of the mechanically embedded three-layer ONIOM(MO:MO:MM) method.31 This method attempts to overcome the drawbacks of a mechanically embedded two-layer ONIOM(MO:MM)30 by introducing a buffer (middle) layer, which is treated by an appropriate lower-level QM theory (e.g., semi-empirical molecular orbital theory), which is computationally less expensive than the method used for the innermost primary subsystem. The second QM layer is designed to allow a consistent treatment of the polarization of the active center by the environment. The new treatment does improve the description, but, with mechanical embedding, it does not solve the problem completely, since the QM calculation for the first layer is still performed in the absence of the rest of the atoms.
II.B. Electrostatic Embedding?
In contrast to an ME scheme, an EE scheme does not require the MM electrostatic parameters for the PS atoms, because the electrostatic interaction between PS and SS is now treated at a more advanced level by including certain one-electron terms in the QM Hamiltonian. The polarization of the PS by the charge distribution of the SS is also taken into account automatically. The recent progress in the development of electrostatic embedded ONIOM method38 reflects the trend of moving from ME to EE in QM/MM methodology. The price to pay for this improvement is more complicated implementation and increased computational cost.
The unsolved issue for EE schemes is how to construct the one-electron terms in the effective QM Hamiltonian. The simplest way is to represent the charge distribution of the SS as a background of atom-centered partial charges. This is further facilitated by the availability of a set of pre-parameterized MM point charges in many MM force fields; these MM point charges have in principle been parameterized consistently with the other MM parameters to give accurate MM energies, and they have been validated by extensive test calculations. The use of these MM atom-centered partial charges is very efficient, and it is the most popular way in constructing the effective QM Hamiltonian. Nevertheless, the question is raised: are charge parameterized for a particular MM context also appropriate for use in a QM Hamiltonian?
The MM point charges actually include the contributions due to higher-order multipoles implicitly, i.e., the higher order contributions are folded into the zero-order parameters. By considering higher order multipole contributions explicitly, one might increase the accuracy of calculated electrostatic interactions, but this makes the implementation more difficult, and the computational costs grow. The development of distributed multipole parameters is also a difficult and time-consuming task, but the biggest obstacle is that the higher-order terms are generally sensitive to the geometry or conformation changes.113-115 The high conformation-dependence of the multipole expansion limits the transferability.116 For example, only about 20 amino acids are commonly encountered in proteins. It would be ideal to have one set of parameters for these 20 amino acids, which could be used to simulate any proteins, and it would be very inconvenient if one had to develop a new set of parameters whenever another protein is studied or whenever the conformation of a given protein changes considerably.
Another unsolved issue in ascertaining the best EE strategy is the question of the polarization of the SS. In principle, the PS and SS will polarize each other iteratively until their charge distributions are self-consistent. Ideally, an EE scheme should be able to handle such this self-consistency; but usually the charge distribution of the SS is considered frozen for a given set of SS nuclear coordinates. Schemes that relax this constraint can be called self-consistent embedding schemes (or polarized embedding schemes). However, self-consistency is difficult to achieve, because it requires a polarizable MM force field, which has the flexibility to respond to perturbation by an external electric field. Such flexibility is not available in today’s most popular MM force fields, although research to develop a polarizable force field has received much attention.117 Moreover, the use of a self-consistent embedding scheme also brings additional complication to the treatment of the boundary between the PS and SS, which we will discuss later in next section. Finally, it increases the computational effort, since iterations are required to achieve self-consistent polarization of the PS and SS. Thus, in most EE implementations, the PS is polarized by the SS, but the SS is not polarized by the PS. Early examinations on the self-consistent embedding scheme was carried out by Thompson and Schenter43 and Bakowies and Thiel.45 Their treatments are based on models that describe the mutual polarization of QM and MM fragments in the sprit of reaction field118,119 theory, with the difference that the response is generated by a discrete reaction field (atomic polarizabilities) rather than a continuum. Their results suggests that the polarization of the SS by the PS can be crucial in applications involving a charged PS that generates large electric fields.
II.C. Interactions
Other than Electrostatic
Although, as discussed above, the key difference between the ME and EE schemes is the treatment of the electrostatic interaction between the PS and the SS, there are also important issues involving in the treatments of the other interactions between the PS and the SS. These interactions include the bonded (stretching, bending, and torsional) interactions and the non-bonded van der Waals interactions, which are handled at the MM level.
A similar question arises here, as in the case of electrostatic interactions for the ME scheme, but now even for the EE schemes, i.e., all the interactions calculated at the MM level rely on the availability of MM parameters for the PS atoms. These parameters are not necessarily the same for the PS atoms in the reactant and product because the atom types are changed for some atoms, e.g., a carbon atom may change from C=O type to C-O-H type. Which set of MM parameters should we use? Should one switch between two sets of MM parameters during a dynamics calculation following the reaction path? Switching between these two sets of parameters during a dynamics calculation or along the reaction path is not convenient, and, again, avoiding this was the one of the reasons for moving up from MM to QM. Moreover, even if the switching between parameters could be done, one does not know at which point along the reaction path it should be done and how suddenly if the change is gradual. There is no unambiguous answer.
One key difference between the need for non-bonded electrostatic parameters and the need for bonded parameters is that the latter requirement can always be obviated by making the PS bigger, i.e., moving the QM-MM boundary out. The change of atom types might change the force constants for associated bonded-interactions. Usually force constants for stretches are much bigger than force constants for bends, and force constants for torsions are the smallest. The changes of force constants due to the change of atom types are often in this order, too. This provides us with gauge for monitoring the error due to using a single set of MM parameters. The bonded interactions between PS and SS are localized at the boundary. In principle, the use of a larger PS pushes the boundary away from the reaction center and helps to alleviate the uncertainty due to parameter choices, but at a price of increasing computational effort. In many cases, though, enlarging the PS is not a practical solution. What then? Our suggestion is to keep using one set of MM parameters, and examine whether the errors introduced by using one set of parameters exceeds the errors produced by other approximations that are introduced by the QM/MM framework. Although our treatment is not a perfect solution, it is very practical, and it appears to be reasonable.
For the van der Waals interactions, any PS atoms that change atom types are intrinsically ambiguous; this problem cannot be avoided even if a larger QM subsystem is adopted. Fortunately, in practice, it does not appear to be a serious problem in most cases, since the van der Waals interactions are significant only at short distances, and the use of only one set of van der Waals parameters is often adequate.
II.D. Treating
Periodic Systems
So far we have been talking about QM/MM methodology in a very general sense. An interesting issue that we are now going to address is how to treat periodic systems. This is especially important in modeling of solid-state materials such as metal and metal oxide and surface-adsorbates systems. Excellent discussions 76,95,99 of this aspect are available, and thus we only briefly discuss the studies on zeolites.
As we mentioned above, the most important interaction between the PS and the SS is the electrostatic interaction. Thus, the central problem in treating periodic systems like the zeolite-substrate systems is how to incorporate the long-range electrostatic interactions between the SS and PS into a cluster model. The basis idea99 is to develop a charge distribution with a finite number of multipoles (usually point charges) to mimic the infinite and periodic charge distribution of the environment in which the cluster model is embedded. This effective charge-distribution can be obtained by minimizing the difference between the electrostatic potentials that are generated by the effective charge distribution and by the original infinite and periodic charge distribution at a set of sampling grids at the active site. Additional effective core potentials can be associated with selected point charges if needed. By doing so, one truncates the infinite and periodic system to a finite embedded cluster model, which is now much easier to handle.
III. QM/MM
Boundary Treatment
In this section, we examine the
problem with a stronger microscope, and we consider details, especially for the
troublesome implementation of the EE scheme. In some cases, the boundary
between PS and SS does not go through a covalent bound, e.g., a molecule being
solvated in water, where the solute is the PS and the solvent (water) molecules
is the SS.23,57 The effective fragment potential method79 can also be considered as a special case of
MM in this catalog. In many cases, however, one cannot avoid passing the
boundary between the PS and SS through covalent bonds (e.g., in enzymes or
reactive polymers) or through ionic bonds (in solid-state catalysts). This is
called cutting a bond. In such cases, special care is required to treat the
boundary, and this section (Section III) is mainly concerned with this problem.
III.A. Link Atom or Local Orbital?
Treatments of the boundary between PS and SS regions can be largely grouped into two classes. The first is the so-called link atom approach, where a link-atom is used to saturate the dangling bond at the “frontier atom” of the PS. This link atom is usually taken to be a hydrogen atom,22,30,31,33,35-37 or a parameterized atom, e.g., a one-free-valence atom in the “connection atom”,48 “pseudobond”,87 and “quantum capping potential”88 schemes, which involve a parameterized semi-empirical Hamiltonian48 or a parameterized effective core potential (ECP)87,88 adjusted to mimic the properties of the original bond being cut. The second class of QM/MM methods consists of methods that use localized orbitals at the boundary between the PS and SS. An example is the so-called local self-consistent field (LSCF) algorithm,25-29 where the bonds connecting the PS and SS are represented by a set of strictly localized bond orbitals (SLBOs) that are determined by calculations on small model compounds and assumed to be transferable. The SLBOs are excluded from the self-consistent field (SCF) optimization of the large molecule to prevent their admixture with other QM basis functions. Another approach in the spirit of the LSCF method is the generalized hybrid orbital (GHO) method.60,62-64,67,68,65,70 In this approach, a set of four sp3 hybrid orbitals is assigned to each MM boundary atom. The hybridization scheme is determined by the local geometry of the three MM atoms to which the boundary atom is bonded, and the parametrization is assumed to be transferable. The hybrid orbital that is directed toward the frontier QM atom is called the active orbital, and the other three hybrid orbitals are called auxiliary orbitals. All four hybrid orbitals are included in the QM calculations, but the active hybrid orbital participates in the SCF optimizations, while the auxiliary orbitals do not.
Each kind of boundary treatment has its strength and weakness. The link atom method is straightforward and is widely used. However, it introduces the artificial link atoms that are not present in the original molecular system, and this makes the definition of the QM/MM energy more complicated. It also presents complications in optimizations of geometries. In addition, it is found, at least in the original versions of the link atom method, that polarization of the bond between the QM frontier atom and the link atom is unphysical due to the nearby point charge on the MM “boundary atom” (an MM boundary atom is the atom whose bond to a frontier QM atom is cut). The distance between the link atom and the MM boundary atom is about 0.5 Å in the case of cutting a C-C bond (the bond distance is about 1.1 Å for a C-H bond and about 1.5 Å and for a C-C bond). Similar problem is found in the case of cutting a Si-O bond (the bond distance is about 1.4 Å for a Si-H bond and about 1.6 Å and for a Si-O bond). At such a short distance, the validity of using a point charge to represent the distribution of electron density is questionable. Special treatments are applied to the MM charges near the boundary so as to avoid this unphysical polarization.21,45,48,52,73,87,97,91 We will discuss this problem in more detail later Subsection III.B.
The methods using local orbitals are theoretically more fundamental than the methods using link atoms, since they provide a quantum mechanical description of the charge distribution around the QM/MM boundary. The delocalized representation of charges in these orbitals helps to prevent or reduce the over-polarization that, as mentioned above, is sometimes found in the link-atom methods. However, the local-orbital methods are much more complicated than the link-atom methods. The local-orbital method can be regarded as a mixture of molecular-orbital and valence-bond calculations; a major issue in these studies is the implementation of orthogonality constraints of MOs.67 Moreover, additional work is required to obtain an accurate representation of the local orbitals before the actual start of a QM/MM calculation. For example, in the LSCF method, the SLBOs are pre-determined by calculations on small model compounds, and specific force field parameters are needed to be developed to work with the SLBOs. In the GHO method, extensive parameterization for integral scaling factors in the QM calculations is needed.60,67,68,65,70 Such parameters usually require reconsideration if one switches MM scheme (e.g., from CHARMM to OPLS-AA), QM scheme (e.g., from semi-empirical molecular orbital methods to density functional theory or post-Hartree-Fock ab initio methods), or QM basis set. The low transferability limits the wide application of the local orbital methods.
The performance of both the link-atom and local-orbital approaches has been examined by extensive test calculations. The conclusion is that reasonably good accuracy can be achieved by both approaches if they are used with special care. It is expected that development and application of both the link-atom and local-orbital methods will continue in the future.
III.B. Using
Link-Atom Methods
A central objective in the development of an universal QM/MM algorithm is to make the algorithm as general as possible and to avoid or to minimize the requirement of introducing any new parameters. Thus, for example, one way to define a universally applicable method would be that, when one makes an application to a new system, no MM parameters need to be changed, no QM integral scaling factors needed to be determined, no effective core potentials (ECP) needed to be developed. From this point of view, the link-atom method seems very attractive. Furthermore the method will be more easily built into a standard QM code if the link atom is an ordinary hydrogen atom with a standard basis set. Methods having these features will be examined in more detail in this section.
To facilitate our further discussion, we will label the atoms according to “tiers”. The MM boundary atom will be denoted as M1. Those MM atoms directly bonded to M1 will be called second-tier molecular mechanics atoms or M2; similarly, one defines M3 atoms as those MM atoms bonded to M2 atoms … The QM boundary atom that is directly connected to M1 is labeled Q1. Similarly, one defines Q2 and Q3 atoms in the QM subsystem. We will denote the link-atom as HL, which stands for “hydrogen-link”, emphasizing that an ordinary hydrogen atom is used/preferred.
III.B.1. Location of the Link-Atom
As we mentioned in the previous section, the link-atom method has its problems. The first problem is the introduction of the coordinates of the link atom, which are extra degrees of freedom. By definition, a link atom is neither a QM nor an MM atom, because it is not present in the original PS or SS. This causes ambiguity to the definition of QM/MM energy for the ES. One way to avoid this problem is to make the coordinates of a link atom depend on the coordinates of the PS frontier atom and the SS boundary atom, i.e., the Q1 and M1 atoms. Such a constraint removes the extra degrees of freedom due to the link atom. Usually the link-atom is put on the line that connects the corresponding Q1 and M1 atoms. Morokuma and coworkers33,120 proposed to scaled the Q1-HL distance R(Q1-HL) with respect to the Q1-M1 distance R(Q1-M1) by a scaling factor CHL:
R(Q1-HL) = CHL R(Q1-M1) (3)
During a QM/MM geometry optimization or a molecular dynamics of reaction path calculation, the equilibrium Q1-HL and Q1-M1 distances are constrained to satisfy equation (3). The scaling factor, CHL, depends on the nature of the bonds being cut and constructed. It has been suggested33 that it should be the ratio of standard bond lengths between Q1-HL and Q1-M1 bonds, which is close to 0.71 for replacement of a C-C single bond by a C-H bond. This treatment is reasonable, and its simplicity facilitates implementation of analytic energy derivatives (gradient and Hessians). However, the meaning of “standard bond length” is ambiguous. Our treatment is to set the scaling factor by
CHL = R0(Q1-H) / R0(Q1-M1), (4)
where R0(Q1-H) and R0(Q1-M1) are the MM bond distance parameters for the Q1-H and Q1-M1 stretches in the employed MM force field, respectively.
It is worthwhile to mention that Eichinge et al.81 also proposed a scaled-bond-distance scheme that is similar to the above scheme by Morokuma and coworkers. However, the scheme by Eichinge et al. makes the scaling factor depends on the force constants of the C-C stretch and C-H stretch instead of the bond distances, and it introduces several additional terms to correct the energy.
III.B.2. MM Charges near the Boundary
Another problem (in fact, the problem that has caused the most concern) for the link atom method, as we mention in the previous section, is the over-polarization of the Q1-HL bond due to the nearby M1 point charge. The main reason is that at such a short distance (usually about 0.5 Å in the case of cutting a C-C bond and about 0.2 Å in the case of cutting a Si-O bond), a point charge assigned to the M1 nucleus does not provide a good approximation for the smeared distribution of charge density. For nearby charge distributions, one must considers screening and charge penetration, and dipole or higher order multipole moments can also become important. Various approaches have been attempted to avoid or minimize this over-polarization effect, and they are outlined below.
If a scheme does nothing to modify the MM charges, we label the scheme as straight-electrostatic-embedding (SEE). The SEE scheme causes the over-polarization problem.
The
simplest way to avoid over-polarization is to ignore the M1 charge by setting
it to zero;121 we call this method the Z1
scheme. One can also zero out both M1 and M2 charges; the method can be called
Z2. If all M1, M2, and M3 charges are omitted,21 the scheme is called Z3. The
Z3 scheme is the default option for electrostatic embedding in the ONIOM
calculations in Gaussian03;122 but Gaussian03 also
allows one to use scaling factors other than zero for M2, M2, and M4 charges
(the M1 charge is always set to zero). The scaled-charge schemes are
generalizations of the eliminated-charge scheme. Schemes that eliminate or
scale MM charges often result in changing the net charge of the SS, e.g., a
neutral SS might become partially charged,
and generate artifacts in the calculation of energies or spurious long-range
forces.
In many force fields such as CHARMM, the neutrality of certain groups is enforced during the parameterization by imposing a constraint that the sum of charges for several neighboring atoms is zero. An improved eliminated-group-charge scheme47 takes advantage of this feature by deleting the atomic charges for the whole group that contains the M1 atom. This ensures that the net charge of the SS does not change. It has been found that this scheme is more robust than the Z1, Z2, and Z3 schemes because it preserves the charge for SS.
A shifted-charge scheme96 has been developed to work with force fields where the neutral-groups feature is not available. (Of course, the scheme can also be used for force fields having the neutral-groups feature). In this scheme, called the Shift scheme, the M1 charge is shifted evenly onto the M2 atoms that are connected to M1, and an additional pair of point charges is placed in vicinity of the M2 atom in order to compensate for the modification of the M1-M2 dipole by the initial shift.
As pointed out above, the over-polarization effect is largely due to the poor approximation for the distribution of charge density around the M1 atom by a point charge. Therefore, one might think of using a more realistic description for the charge distribution. Recently, it has been proposed52,91 to use Gaussian charge distributions instead of point charges for selected atoms.
|
|
|
|
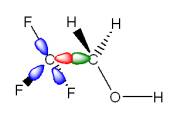
Fig. 2. The redistributed charge scheme
(right) is a molecular mechanical analog to the quantal description by the
generalized hybrid orbital (GHO) theory (left). The MM boundary atom and the
active hybrid orbital (shown in red) in the GHO theory are now modeled by an
H atom, and the auxiliary orbitals (shown in blue) are modeled by three point
charges. |
|
Recently, we69 developed two new schemes: a redistributed-charge (RC) scheme and a redistributed-charge-and-dipole (RCD) scheme, which are based on combining the link-atom treatment and the local-orbital treatment. As indicated in Fig. 2, both schemes use redistributed charges as molecular mechanical mimics of the auxiliary orbitals associated with the MM boundary atom in the GHO theory. In the RC scheme, the M1 charge is distributed evenly onto mid-points of the M1-M2 bonds, i.e., at the nominal centers of the bond charge distributions. The redistributed charge and M2 charges are further modified in the RCD scheme to restore the original M1-M2 bond dipole. The RC and RCD schemes handle the charges in ways that are justified as molecular mechanical analogs to the quantal description of the charge distribution offered by GHO theory.
IV. Validation of a QM/MM
Algorithm
Validating QM/MM methods by comparing to high-level calculations or experiment is essential, since the use of unvalidated methods is unacceptable. Although the motivation for developing QM/MM methods is to apply them to large systems (e.g., reactions in the condensed phase, including liquids, enzymes, nanoparticles, and solid-state materials), most of the validation studies have been based on small gas-phase model systems, where a “model system” is a small- or medium-sized molecule. It is important, in interpreting such validation tests, to keep two important issues in mind.
First, the molecular mechanics parameters, especially partial charges, are usually designed for treating condensed-phase systems where partial charges are systematically larger due to polarization effects in the presence of dielectric screening; thus electrostatic effects of the MM subsystem may be overemphasized in the gas phase. Special attention is given to alkyl groups that are frequently involved in these test examples, because a non-polar C-C bond is often considered to be the most suitable place for putting the QM/MM boundary. An alkyl group in the gas phase appears to be very unpolar, and the C and H atoms are often assign atom-center point charges of small values. For example, in a recent study,69 charges for the C and H atoms in a C2H6 molecule are –0.05 e and 0.02 e, respectively, as derived by the Merz-Singh-Kollmann21,123 electrostatic potential (ESP) fitting procedure. An alkyl group becomes more polar in water or in other polar solvents, and the point charges on the atoms in the alkyl group increase significantly. The OPLS-AA force field would assign a charge of –0.18 e for each C atom and 0.06 e for each H atom in the C2H6 molecule, and in the CHARMM fore filed the values are even large (–0.27 e for each C atom and 0.09 e for each H atom). Our calculations69 on the proton affinity of several gas-phase molecules having alkyl groups found much bigger error when using the charges developed for simulations in water than when using the ESP-fitted charges. We believe that our conclusion is general since we tested several QM/MM schemes that treat the MM charges near the boundary differently, and observed a similar trend. We learned from this that it is very hard to test schemes designed for complex processes in the condensed phase by carrying calculations on small molecules in the gas phase.
It is probably more important to focus on the fact that the QM/MM interface can introduce artifacts. Thus, the main goal of validation tests should usually be to ensure that no unacceptably large energetic or structural artifacts are introduced, rather than to achieve high quantitative accuracy for MM substituent effects. In this regard, a QM/MM method is often tested by examples that are more difficult in one or another sense than those in a normal application, because one wants to know where the performance envelope lies. Thus, calculations on examples having large proton affinities are very suitable for testing. Proton or hydride transfer involves significant charge transfer and is thus a crucial test for the treatment of electrostatic interactions (especially the procedure for handling MM charges near the QM/MM boundary) in a QM/MM method. A large value of the energy difference between the reactant and product also helps us to draw conclusions that are not compromised by the intrinsic uncertainty of the QM/MM approach.
The proton affinity of CF3CH2O-, where CF3 is the SS and CH2O- is the PS, is one of these difficult examples, due to both the close location of the reaction center to the boundary and the presence of significant point charges on the atoms in the CF3 group near the boundary. A recent study69 on this difficult example by making comparisons between full QM computations and various QM/MM schemes with the ESP-fitted MM charges for the CF3 group. The QM/MM schemes include the capped PS, the SEE scheme, three eliminated-charge (Z1, Z2, and Z3) schemes, the Shift scheme, the RC scheme, and the RCD scheme. It is found that the Shift and RCD schemes, both of which preserve both the charge of the SS and the M1-M2 bond dipoles, are superior to the other schemes in comparison. For example, when, the errors for the RC and Shift schemes are 1 and 2 kcal/mol, respectively. It is also found that the largest error is caused by the Z1 scheme (75 kcal/mol), where neither the charge nor the dipole is preserved. The results suggest that it is critical to retain the feature of charge distribution near the QM/MM boundary. In line of this conclusion, the SEE scheme does not seem to be too bad with an error of 9 kcal/mol; actually it is even better than the RC scheme (error of 12 kcal/mol) and the best charge-eliminated schemes Z2 and Z3 (errors of 25 kcal/mol). However, the error in the optimized Q1-M1 (C-C) distance is 3 to 4 times larger for the SEE scheme than for any of the other schemes to which comparison was made, and this makes the SEE scheme a poor choice in practical applications.
V. Implementation and Software
As summarized in a recent review article, there are basically three kinds of programming architecture for implementing QM/MM methods.
1. Extension of a “traditional” QM package by incorporating the MM environment as a perturbation. Many QM packages are have added or are adding the QM/MM options. A well-known example is the ONIOM method implemented in Gaussian03 (http://www.gaussian.com/). Other examples include the adf (http://www.scm.com/), chimiste/mm (http://www.lctn.uhp-nancy.fr/logiciels.html), mcqub (http://www.chem.umn.edu/groups/gao/software.htm), molcas (http://www.teokem.lu.se/molcas/), mozyme (http://www.chem.ac.ru/Chemistry/Soft/MOZYME.en.html), and QSite (http://www.schrodinger.com/Products/qsite.html) packages.
2. Extension of a “traditional” MM package by incorporating a QM code as a force-field extension. Examples include amber (http://amber.scripps.edu/), charmm (http://www.charmm.org/), and cgplus (http://comp.chem.umn.edu/cgplus/).
3. A central control program interfacing QM and MM packages, where users can select between several QM and/or MM packages. For example, chemshell (http://www.cse.clrc.ac.uk/qcg/chemshell/) and qmmm (http://comp.chem.umn.edu/qmmm/) belong to this catalog.
Each kind of program architecture has its own
merits and disadvantages. The options based on extension of traditional QM
and/or MM packages can make use of the many features of the original program,
for example, the ability of the MM program to manipulate large, complex
biological systems. The disadvantage is that both options need modification of
the codes.
The third option is based on module
construction and is more flexible. It often needs no or little modification on
the original QM and MM programs. The program is automatically updated when the
QM or MM packages that it interfaces are updated. The drawback is that it
requires a considerable amount of effort to transfer the data between the QM
and MM packages, which is usually done by reading data from files, rearranging
the data, and writing the data to files. Such additional manipulations can
lower the efficiency.
Our recently developed program qmmm adopts the third architecture of programming. The qmmm program currently interfaces Gaussian03 for doing QM computations and tinker for doing MM calculations. Geometry optimization and transition-state searching can be done by using the algorithm built into the qmmm program or by using an optimizer in the Gaussian03 program via the external option of Gaussian03. In addition to the RC and RCD schemes, the qmmm program also implements several other schemes such as the SEE, scaled-charge, and shifted-charge schemes for handling the MM point charges near the QM/MM boundary. Currently we are working on combination of the qmmm program with the molecular dynamics program polyrate (http://comp.chem.umn.edu/polyrate/) for doing QM/MM direct dynamics calculations.124
VI. What do We Learn form a QM/MM Calculation?
As discussed in the introduction, one benefit that QM/MM calculations bring to us is the inclusion of the effect of a chemical environment (secondary subsystem, SS) on the reaction center (primary subsystem, PS). The interactions between a PS and an SS are of two kinds: (1) interactions that are significant even at long range (electrostatic interaction), and (2) interactions that are local (bonded interactions) or are only significant at short range (van der Waals interactions). The electrostatic interactions are usually dominant, as they perturb the electronic structure of the PS, and they often have great effects on energetic quantities such as the reaction energy. The bonded and van der Waals interaction act in other ways; they impose geometry constraints by providing a rigid frame in the active site or lattice site to hold the PS. (In fact, the electrostatic interaction will also affect the equilibrium geometry of the PS.)
A practical way to examine the effect of the environment is to compare quantities such as reaction energies or barrier heights as calculated from an isolated QM model and from a QM/MM model. Usually this shows significant differences for processes that involve significant changes in the charge distribution. The calculations for proton transfer reactions are good examples (see the discussion on the proton affinity in Section IV).
However, one sometimes finds the same or very similar reaction energies and barrier heights from isolated QM model systems and QM/MM model calculations. This is likely to be observed for a reaction without much change transfer, e.g., a radical abstraction reaction. This does not mean that the SS does not affect the PS. In such a case, it is likely that the effect due to the SS is roughly the same for the reactant, transition state, and product, and the cancellation leads to small net effects. An approximate analysis of the effects due to SS can be obtained by an energy-decomposition as follows (see also Fig. 3).
|
|
|
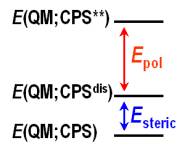
Figure 3. Decomposition of energy due to MM environment into two contributions: the energy due to the polarization by the background point charges (Epol) and the energy due to the geometry distortion (Esteric). See Equations (5) to (8). |
The energy difference between the QM energy for the PS (or CPS, i.e., a PS capped by link atoms) in the gas phase and the QM energy for the PS in an interacting MM environment is defined by
EPS/MM = E(QM;PS**)
- E(QM;PS), (5)
where E(QM;PS**) is the QM energy for the PS embedded in the background point charges of SS, and E(QM;PS) is the QM energy for the PS in the gas phase. In either case, the geometry is fully optimized at the corresponding level of theory, i.e., at the QM/MM level for E(QM;PS**) and at the QM level for E(QM;PS). Equation (5) provides a measure of the magnitude of the perturbation on the QM subsystem due to the MM subsystem. Generally speaking, the two geometries in Equation (5) are different. We further decompose EPS/MM into two contributions: the energy due to the polarization of the background point charges (Epol) and the energy due to the geometry distortion from the PS in the gas phase (Esteric), which are defined as
Epol = E(QM;PS**)
- E(QM;PSdis), (6)
Esteric = E(QM;PSdis) - E(QM;PS),
(7)
EPS/MM = Epol + Esteric, (8)
where E(QM;PSdis) is the gas-phase single-point PS energy for the QM/MM optimized geometry, i.e., one takes the PS geometry that resulted from QM/MM optimization and removes the MM point charges. Although such an energy-decomposition is approximate, it is informative and provides us deeper understanding of the QM/MM calculations.
The energy decomposition is applied to a
reaction that we studied recently69 (Fig. 4).
CH3 + CH3CH2CH2OH à CH4 + CH2CH2CH2OH (R-1)
The PS is CH3 + CH3CH2, giving rise to a CPS as CH3 + CH3CH3. The SS is CH2OH. For each of the reactant, saddle point, and product of this reaction, we found a small steric effect (0.1 kcal/mol) and a dominant polarization effect (9 kcal/mol). It is not surprising to see such a small setic effect, since the distortion of geometry for the CPS from the fully relaxed geometry in the gas phase can be rather small. The critical point is that the energies due to geometry distortion and polarization are so similar along the reaction path that they almost cancel out, giving rise to negligibly small net contributions to the reaction energy and barrier height. Figure 4
|
|
|
|
|
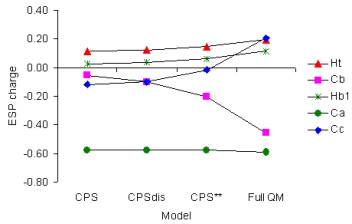
Fig. 4. ESP-fitted charges for selected atoms in
reaction CH3 + CH3CH2CH2OH à CH4 + CH2CH2CH2OH. |
Although the MM environment does not have a large net effect on the relative energies of the H atom transfer reaction (R1), it does have effects on the electronic structure of the CPS through polarization and perturbs the charge distribution. The ESP-fitted charges in Fig. 4 clearly show a trend of stepwise change from the unperturbed CPS (denoted as CPS), to the CPS with distorted geometry (CPSdis), then to the CPS embedded in the background point charge distribution (CPS**), and finally to the ES, as modeled by full QM calculations. It is interesting to note that the Cb-Cc bond seems to be very unpolar according to the CPS calculations, with a small bond dipole pointing from the Cb to the Cc atom. The CPS** calculations predict that the Cb-Cc bond is more polar, with a larger and inverse bond dipole pointing from the Cc to the Cb atom, in qualitative agreement with full QM calculations. The CPS** result is generally closer to the full QM results, suggesting that QM/MM calculations provide a more realistic description for the QM subsystem than the isolated gas-phase QM model calculations.
The conclusion that for a reaction that does not involve much charge transfer, the inclusion of the electrostatic field of the SS will yield small effects in relative energies but large affects in the electronic structure of the PS also gain supports from studies of zeolite-substrate systems.95 In Ref. 95, it has been found that the inclusion of the electrostatic field of the SS slightly alters the barrier (by ca. 2 kcal/mol) of a methyl shift reaction over a zeolite acid site, but has considerably large effects on the charge distribution and vibrational frequencies. For example, the charge on the O atoms is changed by 0.16 e.
V. Where Do We Go from Here?
Combining QM and MM by applying them to
separate subsystems with a boundary in physical space is very natural, and it
is safe to say that it is now a permanent part of the theoretical toolbox.
However, there are other ways to combine QM and MM, and future work may see
greater use of methods that blend QM and MM more intimately.
A venerable example of such an approach is the use of quantum mechanics to suggest new functional forms for molecular mechanics. The oldest example would be the Morse curve, which was originally derived by a QM treatment of H2+.125 Replacing a harmonic bond stretching potential by a Morse curve allows MM to treat bond breaking. It is much harder to treat synchronous bond breaking and bond forming, but this was also accomplished in the early days of quantum mechanics, resulting in the London equation.126-128 Raff129 was apparently the first to combine the valence-bond-derived QM London equation with molecular mechanics terms to make a QM/MM reactive potential, and in recent years many other workers,130-133 especially Espinosa-Garcia and coworkers, have made fruitful use of this technique. Various workers, of whom we single out Brenner134-136 and Goddard and coworkers137-140 for noteworthy systematic efforts, have made generalizations to more complex reactive systems. However, these methods are neither universal nor systematically improvable like the methods discussed in Sections III and IV.
One way to make the combination of valence bond theory and molecular mechanics more universal and systematic is multi-configuration molecular mechanics141-145 (MCMM). MCMM combines QM and MM in a different way than QM/MM; in MCMM the whole system is treated by QM, and simultaneously the whole system is treat by MM. In fact, every atom is treated by two different MM schemes, one corresponding to a reactant and the other to a product, and the two MM energy expansions interact by a 2 ´ 2 configuration interaction matrix highly reminiscent of London’s 2 ´ 2 matrix matrices or the similar 2 ´ 2 matrices used by Raff,129 Warshel and Weiss,146 and others. However, in MCMM the off-diagonal elements of the Hamiltonian are not empirical MM parameters as in previous work, but rather are determined by systematically improvable QM methods. The method is very young but very promising.
In the future, we can expect further progresses in MCMM. One straightforward improvement is to use QM/MM to replace QM in determination of the off-diagonal element of the Hamiltonian matrices, and this scheme can be called QM/MM-based-MCMM, or QM/MM-MCMM for short. Another even more promising scheme is to combine MCMM with MM in the “same way” that QM is combined with MM in combined QM/MM methods. That is, use MCMM to replace the QM in QM/MM; this scheme can be called MCMM-based-QM/MM, or MCMM-QM/MM. Both schemes make MCMM suitable for handling very large system. Work in this direction is in progress, and encouraging preliminary results have been obtained.147
Another area of future improvement is use of improved MM formalisms in QM/MM methods. We have already mentioned polarizable MM force fields (see Section II.B).117 Even without allowing polarization, the charges in MM force fields can be improved in various ways. In particular, various charge models have been developed or are in refinement. Examples include the restrained electrostatic potential148 (RESP) fitting procedure and its latest improved version “dynamically generated restrained electrostatic potential” (DRESP)149 for QM/MM calculations, the family of CMx (x = 1,150 2,151,152 and 3153-155) charge models, the charge equilibration156,157 (CEq) method, and the consistent charge equilibration (CQEq)158-160 method.
Another important trend we can expect to see in the near future is the incorporation in MM of methods for modeling metallic systems that were developed in the physics community. For example, just as simplified valence bond theory can be used to obtain functional forms for extending MM to reacting systems, the second-moment approximation to the tight-binding approximation (also known as extended Hückel theory) can be used to obtain new forms for modeling metals.161 An example of this kind of approach is the use of the embedded-atom functional form to develop MM potentials for Al nanoparticles.162
A theme that emerges from several of the approaches discussed in this section is the difficulty of classifying the potential energy function as QM or MM. For example, is the embedded-atom method an approximate version of density functional theory or is it MM? Is MCMM an automatic fitting method for QM energies or is it an extension of MM to reactive system? We prefer to think of these methods as new kinds of QM-MM hybrids where the QM-MM combination is more intimate than in the first generation of combined QM/MM methods.