Comp Chem Research Developments

Combining Self-Consistent-Charge Density-Functional Tight-Binding (SCC-DFTB) with Molecular Mechanics by the Generalized Hybrid Orbital (GHO) Method

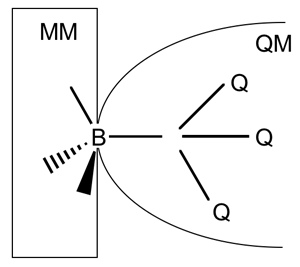
An important goal for computational chemistry is to model the reactivity of even large and complex systems. This can be computationally challenging because the calculation of the potential energy function for reactive systems requires quantum mechanics.  An example of a difficult problem would be the modeling of metalloenzymes containing zinc [1,2], because the coordination shells of zinc often undergo unique and specific coordination shell changes in the active site, including both tetrahedral coordination and pentacoordination [2].  The use of a combined quantum mechanics/molecular mechanics (QM/MM) approach is a powerful tool for studying such problems.

In combined QM/MM calculations, usually only a small part of the reactive system is described by quantum mechanics (QM), and the large remaining subsystem is treated by cost-efficient molecular mechanics (MM).  The use of generalized hybrid orbitals (GHO) at the bond that forms a boundary between the QM and MM subsystems has been shown to provide a well-balanced and stable connection between the QM and MM regions [3].  In a recent paper [4], graduate student Jingzhi Pu, Professor Jiali Gao, and Professor Donald G. Truhlar formulated the GHO algorithm and its analytical gradients for treating the QM subsystem by the self-consistent-charge density-functional tight-binding (SCC-DFTB) theory, which is a highly efficient and accurate semiempirical alternative to density function theory (DFT).  The new GHO-SCC-DFTB method is expected to have a wide variety of applications, such as for study of enzymatic catalysis, non-biological catalysis, and large organic and organometallic molecules.

[1]  See, for example: (a) Alhambra, C.; Corchado, J. C.; Sanchez, M. L.; Gao, J.; Truhlar, D. G. J. Am. Chem. Soc. 2000, 122, 8197; (b) Amin, E.A.; Welsh, W.J. J. Med. Chem. 2001, 44, 3849; (c) Henrich, V. Acc. Chem. Res. 1999, 32, 589.  (d) Elstner, M.; Cui, Q.; Munih, P.; Kaxiras, E.; Frauenheim, T.; Karplus, M. J. Comput. Chem. 2003, 24, 565.

[2]  Dudev, T.; Lim, C. Chem. Rev. 2003, 103, 773.

[3]  (a) Gao, J.; Amara, P.; Alhambra, C.; Field, M. J. J. Phys. Chem. A 1998, 102, 4714. (b) Truhlar, D. G.; Gao, J.; Alhambra, C.; Garcia-Viloca, M. Corchado, J.; Sánchez, M. L.; Villà, J. Acc. Chem. Res. 2002, 35, 341.

[4]  Pu, J.; Gao, J.; Truhlar, D. G. J. Phys. Chem. A 2004, in press.

Fig. 1. Schematic representation of the QM/MM partition in the GHO method.  The GHO boundary atom (usually an sp3 carbon) is denoted as B and is represented by a set of generalized hybrid orbitals.  The QM atom directly bonded to the GHO boundary atom is called the frontier atom and denoted by A. The QM/MM partition is along the covalent bond A-B.

Fig. 2. A tripeptide, Tyr-His-Ala, whose structure has been optimized with the GHO-SCC-DFTB method.  The atoms in the red circle have been treated by quantum mechanics, and those outside the circle have been treated by molecular mechanics.  The GHO boundary carbon atom is marked by a red "star".